Analyses Utility Classes and Functions¶

Utility classes from the analyses package are documented here.

`nodal` – Nodal Analysis¶

This module contains basic classes/functions for nodal analysis. These are part of the standard netlist analyses but they can also be used independently.

class cardoon.analyses.nodal.DCNodal(ckt)¶

Calculates the DC part of currents and Jacobian

Matrices and vectors (G, Jac, s) are allocated here. This is to centralize all allocations and avoid repetitions.

Requires a nodal-ready Circuit instance (ckt) instance (see make_nodal_circuit())

get_guess()¶

Retrieve guesses from vPortGuess in each nonlinear device

Returns a guess vector

get_i(xVec)¶

Calculate total current

returns iVec = G xVec + i(xVec)

xVec: input vector of nodal voltages.

iVec: output vector of currents

get_i_Jac(xVec)¶

Calculate total current and Jacobian

Returns (iVec, Jac):

iVec = G xVec + i(xVec)
Jac = G + (di/dx)(xVec)

xVec: input vector of nodal voltages.

iVec: output vector of currents

Jac: system Jacobian

get_source()¶: Get the source vector considering only the DC source components

refresh()¶

Re-generate linear matrices

Used for parameter sweeps

save_OP(xVec)¶

Save nodal voltages in terminals and set OP in elements

The following information is saved:

The nodal voltage vector for the circuit (self.xop)

The nodal voltage in each terminal (term.nD_vOP)

The control port voltages in each nonlinear device (elem.nD_xOP)

set_ext_currents(extIvec)¶

Set external currents applied to subcircuit

extIvec: vector of external currents. Length of this vector should be equal to the number of external connections. The sum of all currents must be equal to zero (KCL)

This will fail if not a subcircuit

class cardoon.analyses.nodal.TransientNodal(ckt, im)¶

Keeps track of transient analysis equations.

This class only sets up transient equations. Equations are solved elsewhere. Circuit history required for numerical integration is kept by an integration method class.

Matrices and vectors (G, C, JacI, JacQ, s, etc.) are allocated here. This is to centralize all allocations and avoid repetitions.

Requires a nodal-ready Circuit instance (ckt) instance (see make_nodal_circuit()). The circuit is not modified, one circuit can be shared amongst several TransientNodal objects.

accept(xVec)¶: Accept xVec for current time step and store state

get_i(xVec)¶

Calculate total current

returns iVec = G’ xVec + i’(xVec)

xVec: input vector of nodal voltages.

iVec: output vector of currents

get_i_Jac(xVec)¶

Calculate total current and Jacobian

Returns (iVec, Jac):

iVec = G' xVec + i'(xVec)
Jac = G' + (di'/dx)(xVec)

xVec: input vector of nodal voltages.

iVec: output vector of currents

Jac: system Jacobian

get_rhs(ctime)¶

Returns system rhs vector: s’

s’ includes source vector, charge history and convolution contributions

ctime: current time

get_source(ctime)¶

Get the source vector considering DC and TD source components

ctime: current time.

refresh()¶

Re-generate linear matrices

Used for parametric sweeps

set_IC(h)¶

Set initial conditions (ICs)

h: (initial) time step

Retrieves ICs from DC operating point info in elements

update_Gp()¶: Recalculate Gp from im information

update_q(xVec)¶: Recalculate qVec for a given value of xVec

cardoon.analyses.nodal.delay_interp(td, vp, h, tsV, vpV)¶

Use linear interpolation to find v(t-td)

td: time delay vp: current port voltage h: current time step tsV: vector with past time steps vpV: vector with past voltage samples

returns (v(t-td), deriv_coeff)

cardoon.analyses.nodal.make_nodal_circuit(ckt, termList=None)¶

Add attributes to Circuit/Elements/Terminals for nodal analysis

This functionality should be useful for any kind of nodal-based analysis (DC, AC, TRAN, HB, etc.)

Takes a Circuit instance (ckt) as an argument. If the circuit contains the ‘gnd’ node, it is used as the reference. Otherwise an indefinite matrix with no reference is assumed.

If termList is provided, the terminals in that list are assigned the first positions in the NAM matrix. Row/Column numbers for external terminals are stored in the nD_extRClist attribute.

New attributes are added in Circuit/Element/Terminal instances. All new attributes start with nD_

cardoon.analyses.nodal.process_nodal_element(elem, ckt)¶: Process element for nodal analysis

cardoon.analyses.nodal.restore_RCnumbers(elem)¶

Restore RC numbers in internal terminals

Assumption is number of internal terminals is the same

cardoon.analyses.nodal.run_AC(ckt, fvec)¶

Set up and solve AC equations

ckt: nodal-ready Circuit instance (ckt) instance with OP already set

fvec: frequency vector. All frequencies must be different from zero

DC solution not calculated here as it needs special treatment and that solution is already obtained by the OP analysis.

Set results in terminals in vectors named aC_V

Returns a matrix with results. Dimension: (nvars x nfreq)

cardoon.analyses.nodal.set_Jac(M, posRows, negRows, posCols, negCols, Jac)¶: Set current contributions of Jac into M

cardoon.analyses.nodal.set_i(iVec, posRows, negRows, current)¶: Set current contributions of current into iVec

cardoon.analyses.nodal.set_quad(G, row1, col1, row2, col2, g)¶

Set transconductance/transcapacitance quad

G: target matrix

cardoon.analyses.nodal.set_xin(xin, posCols, negCols, xVec)¶: Calculate input port voltage xin

`nodalSP` – Nodal Analysis using Scipy sparse matrices¶

This module contains basic classes/functions for nodal analysis. These are part of the standard netlist analyses but they can also be used independently.

This implementation uses Scipy sparse matrices. By default SuperLU is used to factor the matrix. UMFPack could be used, but SuperLU seems to be faster. The main matrix is built in triplet format (Scipy coo_matrix format).

Many of the functions are directly imported from the nodal module to avoid redundancy. Some of these could be optimized for better performance.

class cardoon.analyses.nodalSP.DCNodal(ckt)¶

Calculates the DC part of currents and Jacobian

Matrices and vectors (G, Jac, s) are allocated here. This is to centralize all allocations and avoid repetitions.

Requires a nodal-ready Circuit instance (ckt) instance (see make_nodal_circuit())

get_guess()¶

Retrieve guesses from vPortGuess in each nonlinear device

Returns a guess vector

get_i(xVec)¶

Calculate total current

returns iVec = G xVec + i(xVec)

xVec: input vector of nodal voltages.

iVec: output vector of currents

get_i_Jac(xVec)¶

Calculate total current and Jacobian

Returns (iVec, Jac):

iVec = G xVec + i(xVec)
Jac = G + (di/dx)(xVec)

xVec: input vector of nodal voltages.

iVec: output vector of currents

Jac: system Jacobian

get_source()¶: Get the source vector considering only the DC source components

refresh()¶

Re-generate linear matrices (and Jacobian structure)

Used for parameter sweeps

save_OP(xVec)¶

Save nodal voltages in terminals and set OP in elements

The following information is saved:

The nodal voltage vector for the circuit (self.xop)

The nodal voltage in each terminal (term.nD_vOP)

The port voltages in each nonlinear device (elem.nD_xOP)

The operating point (OP) information in nonlinear devices

set_Jac(M, Jac, mpidx, mnidx, jacpidx, jacnidx)¶: Set current contributions of Jac into M (in coo format)

set_ext_currents(extIvec)¶

Set external currents applied to subcircuit

extIvec: vector of external currents. Length of this vector should be equal to the number of external connections. The sum of all currents must be equal to zero (KCL)

This will fail if not a subcircuit

class cardoon.analyses.nodalSP.TransientNodal(ckt, im)¶

Keeps track of transient analysis equations.

This class only sets up transient equations. Equations are solved elsewhere. Circuit history required for numerical integration is kept by an integration method class.

Matrices and vectors (G, C, JacI, JacQ, s, etc.) are allocated here. This is to centralize all allocations and avoid repetitions.

Requires a nodal-ready Circuit instance (ckt) instance (see make_nodal_circuit()). The circuit is not modified, one circuit can be shared among several TransientNodal objects.

accept(xVec)¶: Accept xVec for current time step and store state

get_i(xVec)¶

Calculate total current

returns iVec = G’ xVec + i’(xVec)

xVec: input vector of nodal voltages.

iVec: output vector of currents

get_i_Jac(xVec)¶

Calculate total current and Jacobian

Returns (iVec, Jac):

iVec = G' xVec + i'(xVec)
Jac = G' + (di'/dx)(xVec)

xVec: input vector of nodal voltages.

iVec: output vector of currents

Jac: system Jacobian

get_rhs(ctime)¶

Returns system rhs vector: s’

s’ includes source vector, charge history and convolution contributions

ctime: current time

get_source(ctime)¶

Get the source vector considering DC and TD source components

ctime: current time.

refresh()¶

Re-generate linear matrices

Used for parametric sweeps

set_IC(h)¶

Set initial conditions (ICs)

h: (initial) time step

Retrieves ICs from DC operating point info in elements

set_Jac(M, Jac, mpidx, mnidx, jacpidx, jacnidx)¶: Set current contributions of Jac into M (in coo format)

update_Gp()¶: Recalculate Gp from im information

update_q(xVec)¶: Recalculate qVec for a given value of xVec

cardoon.analyses.nodalSP.create_additional_indexes(elem)¶

Creates pre-calculated indexes for nonlinear devices

The following indexes are calculated:

nD_csidx = (cpidx, cnidx, jacpidx, jacnidx) nD_qsidx = (qpidx, qnidx, jacqpidx, jacqnidx)

cpidx, cnidx, qpidx and qnidx are relative to 0 in this element. The final position in the coo matrix is unknown at this time.

Important note: these indexes depend on the order used to insert elements in set_Jac_triplet()

cardoon.analyses.nodalSP.make_nodal_circuit(ckt, termList=None)¶

Add attributes to Circuit/Elements/Terminals for nodal analysis

Similar to nodal.make_nodal_circuit but in addition calls create_additional_indexes()

cardoon.analyses.nodalSP.process_nodal_element(elem, ckt)¶: Process element for nodal analysis

cardoon.analyses.nodalSP.set_Jac_triplet(M, posRows, negRows, posCols, negCols, Jac)¶

Set elements in M

M: target matrix in (dataVec, rowVec, colVec) format (triplet format)

The looping is not optimal but has the advantage that all positive values are inserted first. This simplify index calculation in create_additional_indexes()

cardoon.analyses.nodalSP.set_quad(G, row1, col1, row2, col2, g)¶

Set transconductance/transcapacitance quad

G: target matrix in (dataVec, rowVec, colVec) format (triplet format)

cardoon.analyses.nodalSP.triplet_append(G, val, row, col)¶: Add val at [row, col] position into G matrix (triplet format)

`fsolve` – Nonlinear equation solve functions¶

This module provides the main function that tries different equation solving strategies provided by an object passed as an argument.

A simple Newton method routine is also provided here. In the future we could implement here additional nonlinear equation solving routines.

cardoon.analyses.fsolve.fsolve_Newton(x0, get_deltax, f_eval)¶

Solves a multidimensional non-linear equation with Newton-Raphson’s method. In each iteration the linear system:

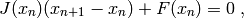
$J(x_n)(x_{n+1}-x_n) + F(x_n) = 0 \; ,$

is solved and a new value for 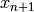$x_{n+1}$ is obtained. Arguments:

x0: initial guess vector

get_deltax(x): function that returns the 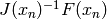$J(x_n)^{-1} F(x_n)$ vector

f_eval(x): function that returns error function vector

Convergence parameters are taken from the global options (Global Options and Constants Tables). Relative and absolute tolerances are checked independently for each variable.

Returns the following tuple: (x, res, niter, success)

x: estimated solution vector at the last iteration

res: maximum residual from all variables

niter: number of iterations

success: True if method converged to specified tolerance, False otherwise

This function originally adapted from pycircuit (https://github.com/henjo/pycircuit)

cardoon.analyses.fsolve.solve(x0, sV, convergence_helpers)¶

Attempt solving circuit equations using several strategies

x0: initial guess

sV: source vector

convergence_helpers: list of functions that can be used to solve equations

Example of helper functions:

solve_simple(x0, sV)
solve_homotopy_gmin(x0, sV)
solve_homotopy_source(x0, sV)

This function originally adapted from pycircuit (https://github.com/henjo/pycircuit)

`integration` – Integration methods for ODEs¶

This module implement different integration methods to be used in transient analysis.

class cardoon.analyses.integration.BEuler¶

Implements Backwards Euler method:

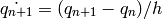
$\dot{q_{n+1}} = (q_{n+1} - q_n) / h$

accept(q)¶: Accept q as last valid value

f_n1()¶: Returns $f_{n-1}(q)$

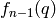
init(h, q)¶

Initialize for integration

Set time step size to h. q is ignored as it is not needed

set_h(h)¶: Change time step size to h

class cardoon.analyses.integration.Trapezoidal¶

Implements Trapezoidal method:

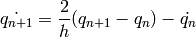
$\dot{q_{n+1}} = \frac{2}{h} (q_{n+1} - q_n) - \dot{q_n}$

accept(q)¶: Accept q as last valid value

f_n1()¶: Returns $f_{n-1}(q)$

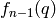
init(h, q, dq=None)¶

Initialize for integration

Set time step size to h, previous charge to q previous derivative to dq

set_h(h)¶: Change time step size to h in next call to f_n1

`sensitivity` – Nodal sensitivity analysis¶

Functions to calculate derivatives for sensitivity analysis. Elements are assumed to have nodal arguments (nD_*).

cardoon.analyses.sensitivity.create_sensitivity_tape(device, parList, inVec)¶

Create sensitivity AD tape

Inputs:

device: device with nodal attributes parList: list of parameters to calculate sensitivities

inVec: input vector including parameters and perhaps nonlinear control voltages at the end of the vector

Side effects: operating point attributes lost in internal terminals

cardoon.analyses.sensitivity.get_i_derivatives(device, parList, xVec, force=False)¶

Returns DC current derivatives with respect to given parameters

Inputs:

device (linear or nonlinear) parList: list of parameters as returned by param.get_float_attributes() xVec: nodal vector force: if True, force tape re-generation

Outputs:

output currents Jacobian

Possible side effect: operating point attributes lost in internal terminals if tape is created

Analyses Utility Classes and Functions¶

`nodal` – Nodal Analysis¶

`nodalSP` – Nodal Analysis using Scipy sparse matrices¶

`fsolve` – Nonlinear equation solve functions¶

`integration` – Integration methods for ODEs¶

`sensitivity` – Nodal sensitivity analysis¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

Analyses Utility Classes and Functions¶

nodal – Nodal Analysis¶

nodalSP – Nodal Analysis using Scipy sparse matrices¶

fsolve – Nonlinear equation solve functions¶

integration – Integration methods for ODEs¶

sensitivity – Nodal sensitivity analysis¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation

`nodal` – Nodal Analysis¶

`nodalSP` – Nodal Analysis using Scipy sparse matrices¶

`fsolve` – Nonlinear equation solve functions¶

`integration` – Integration methods for ODEs¶

`sensitivity` – Nodal sensitivity analysis¶